A Weighty Matter

Here in the USA flight instructor certificates expire after two years. There are several ways to renew; when I was instructing in a charter operation, renewal was a matter of catching the FAA inspector while he was in town, but now I find the most convenient way is through a Flight Instructor Refresher Clinic [FIRC], a 16 hour approved course. The Idaho Department of Aeronautics runs a good one, and Frank Lester rotates them through our rather large state, so everyone gets a chance to attend. Better yet, he offered to let me attend for free in exchange for teaching some of the segments.

When I told my university students that I would spend the weekend attending a 16 hour course they recoiled in horror. When I told them that there would be a test they were impressed.

Usually I believe that what happens in the Pocatello Holiday Inn stays in the Pocatello Holiday Inn, but due to popular demand here are some ideas from my presentation on Weight-and-Balance. The most striking thing to me was the central role of weight in all aerodynamic questions.

---

Glider Nerd Calculations

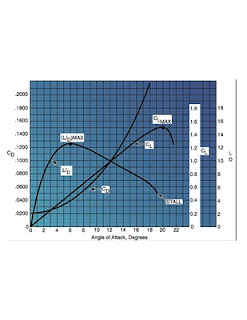
Consider a 3000 pound airplane in level flight at constant airspeed at 100 knots (true airspeed). A reasonable lift-to-drag (L/D) ratio might be 10; see the graph above, taken from The Pilot's Handbook of Aeronautical Knowledge. In level flight, thrust and drag are equal, as are weight and lift, so we have 3000 pounds of lift. Since L/D = 10, this translates into 300 pounds of thrust or drag, depending on your outlook on life.

An airspeed of 100 knots is just about 10,000 ft/sec, which translates into a (300 x 10000)/33000 = 91 Brake Horsepower required.

Rate of Climb depends on excess thrust. Most people don't appreciate this until they study multiengine aerodynamics, but it applies as well here. The formula is

where E is excess thrust and W is weight. Suppose that the airplane has
140 HP available, which is reasonable for a normally-aspirated engine at altitude. Then the excess thrust is 140 - 91 = 49 HP, and the rate of climb is

Change the weight to 4000 pounds, however; the L/D does not change (it's a property of the wing), and now we have (400 x 10000)/33000 = 121 Brake Horsepower required. The excess thrust is down to 19 horsepower, and the rate of climb becomes 156 ft/min.

---

Why do multiengine pilots learn this? Take the 4000 pound airplane at 100 KTAS and give it 400 horsepower available; this is about right for a Seneca. When both engines are turning there are 279 HP of excess thrust available, for a whopping 2300 ft/min climb. Yee-haw! But kill one engine and the excess thrust available is now 79 horsepower, and the rate of climb is down to 650 ft/min. This isn't bad (4000 pounds is light for a Seneca), but the drag picture is a lot worse, too, so L/D has gone down and there is even less excess thrust. The point is that losing half the power costs you WAY more than half the climb!


Change the L/D to 8 and the weight to 4500. Now, at 100 knots, the horsepower required goes up to 170; with only one engine turning there are 30 HP of excess thrust, for a rate of climb of 125 ft/min. At 100 knots you travel forward 10,000 feet in one minute, and the climb gradient is an anemic 75' per nautical mile; the climb angle is less than half a degree.

(Why is the elevation relevant? At higher density altitude the same indicated airspeed corresponds to a higher true airspeed, and hence to more horsepower required.)

I took my Multi-engine Instructor flight test in a Seneca on a hot day at about 4500' MSL. Even though it was in a Seneca (so I had sea level power), when I demonstrated an engine failure to the examiner the airplane would not climb. I headed out across the desert and finally found a thermal that took us to pattern altitude. The moral of this story: always think like you have an even number of engines!

Foolin' Around

We were really just foolin' around, headed to our EAA chapter meeting. My friend had called and offered a ride in his airplane. It wasn't instruction, just a ride.

"You fly, I'm going to take advantage of this chance to play with my new GPS," I said. And, given the luxury of being a passenger, I put my head down. I was reading IFR plates off my iPhone and setting up the approach in the GPS. And taking pictures with his camera.

As we turned downwind, the radio crackled "Blackfoot traffic, Cessna [whatever], taking runway 1 9 for departure."

We both looked up, trying to find the traffic. Was that the Cessna or the numbers? It was almost dusk, and hard to see. My friend asked the Cessna where he was, and he claimed to be well clear.

We turned base. I looked down at the GPS to check the extended centerline.

We turned final. I scanned the panel, out of habit. After all, I was a passenger.

"Hey," I asked, "how come we don't have any green lights?"

We went around and did the pattern right. The wheels felt good on the pavement.

Karma

The weather looked a little iffy so I had filed IFR the night before. In the morning the weather was good, but I decided to fly the trip IFR anyway.

At the hold short line I called "ready." The tower told me to hold for release due to an inbound SkyWest Brasilia. Before i could say "I'll depart VFR," though, the Brasilia cancelled IFR.

Now I was in karmic debt.

Fifteen miles from the destination Center cleared me to climb so he could release a SkyWest RJ. "How about `cancel IFR'?" I came back. "Those are the magic words!" he replied, and I continued my descent.

SkyWest cancelled for me. I cancelled for SkyWest. Now I was in karmic balance.